XRF SumPeak Processing
Sum Peaks[edit | edit source]
Background[edit | edit source]
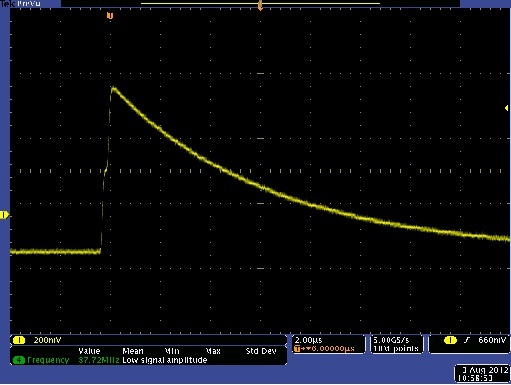
Sum peaks are a result of to xray photons arriving at the detector at the same time. The pulse energy that is measured is twice the energy of a single photon, hence the name sum peak. The FP algorithm attempts to remove the sum peaks but finding the primary peak and then subtracting signal from the area of the spectrum double the primary peak energy.
Here you can see a single pulse, happens to be silver:
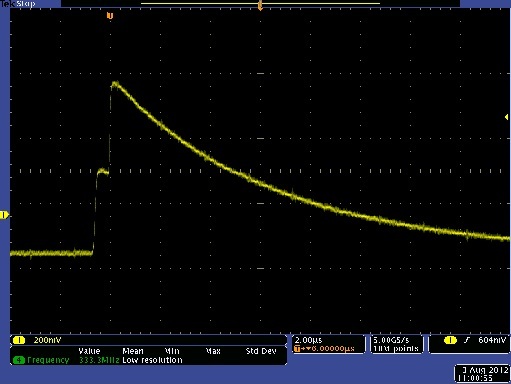
Now, are a couple of views of two pulses creating a sum peak.
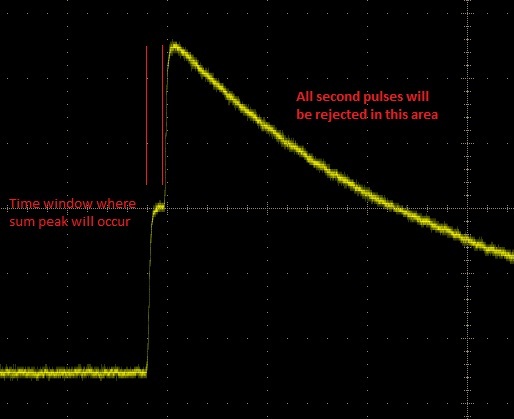
If a second pulse occurs very early after the start of the first pulse, it will be accepted by the pulse processor and will show up in the spectra. If the pulse occurs slightly later then the second pulse will be rejected and will not show up as a peak in the spectra. This means that our post processing is the only way we have of determining if a peak is a true peak or a sum peak.
Correcting for sum peaks[edit | edit source]
In our software we have a parameter called <code>pulsePileUpConstant</code> which is used to "remove" the sum peak from the spectra. This value, in theory is fixed for a single detector with each detector having a different value. The formula for using this constant (tau) is:
N(sum) = (1 / tau) * N2
which means that as the constant is made larger the reduction effect on the sum peak is smaller.
Question[edit | edit source]
Is the sum peak effect truly fixed for a given system? I believe No. The reason is as you raise the count rate, increase tube current in our case, the probability of two pulses occurring to create a sum peak will increase as well, and our pulse processor has an "acceptance window" which is fixed in time. Therefore the intensity of the sum peak should grow faster than the increasing count rate.
According to Stan, the equation N(sum) = 1/tau * N*N does take into account the fixed window. I still believe there maybe a problem with variable count rate, but I'm going to need to collect some data to prove this.
Software info[edit | edit source]
In the file <code>SPI.c</code> we define the <code>pulsePileUpConstant</code> used in the software. The constant is equal to tau in the formula N(sum) = 1/tau * N*N. Note that we are determining a unique value based on <code>fShapeTime</code> or peaking time.